Original algorithm Inspired by previous bird flock simulations framed within the field of social psychology. However, the swarm behaviour is no longer flock-like or school-like but rather swarm-like.
Generalised to n-dimensional, collision-free spaces (for problem-solving | optimisation). Acceleration by distance to an individual attractor and to a social attractor, affected by independent random weights to introduce creativity into the system. In the classical versions, random weights are generated from uniform distributions.
The Intelligent behaviour or the ability to optimise are not programmed but emergent from local interactions. Solutions are sought without using programmer’s expertise on the subject matter.
Classical Update Difference Equation
This governs the update of the state variables (position, velocity) of each particle influenced by its current velocity (or previous position), its current position, a position in the particle’s memory, and a position in the collective memory of its neighbourhood. This includes three control parameters and two independently-generated stochastic weights.
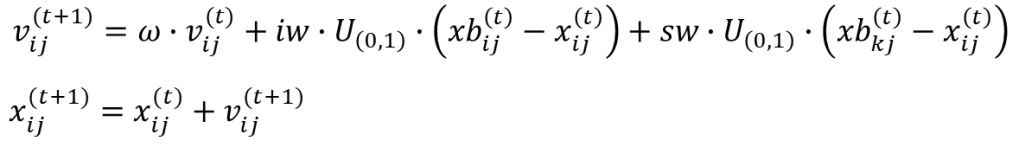
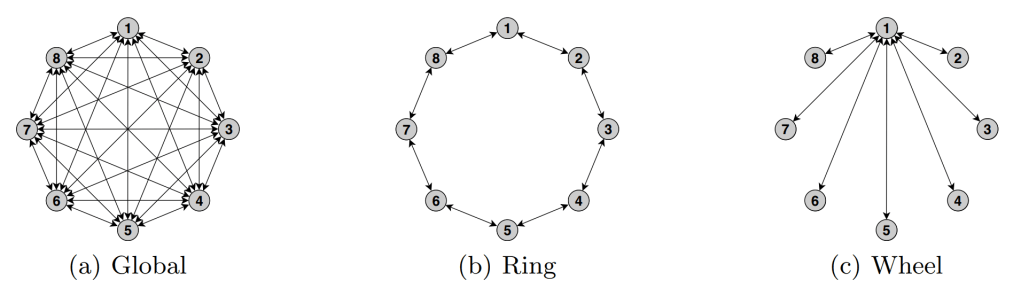
Neighbourhood Topology (Sociometry)
This defines how the information is shared/spread over the swarm.
Three classical neighbourhood topologies are shown below:
Constraint-Handling
The original Particle Swarm Optimisation (PSO) algorithm is suitable for unconstrained problems. The first approach to handle constraints consisted of simply banning from memory any infeasible solution—where therefore cannot constitute an attractor. Subsequent approaches include the Penalty Method (penalising the quality metrics of infeasible solutions), managing tolerances for constraint violations, and setting rules for the comparison between candidate solutions.
